原创 刘宇 集智俱乐部

导语
智能体在理解和处理信息时,本质上是在寻找最有效的压缩方式。这个观点与算法信息论密切相关。最近关于大语言模型的研究表明,语言建模和压缩可能是等价的。可以用大模型做无损压缩,反过来,也可以用压缩机做生成——即“压缩即智能”。在集智俱乐部,北京师范大学珠海校区副教授刘宇做了主题为的分享,介绍如何结合算法信息论中的柯式复杂度和压缩算法来定义距离,并在机器学习、生命、智能等领域展开应用。本文整理自刘宇老师在此次读书会中的分享。
研究领域:算法信息论,柯式复杂度,压缩算法,大语言模型,标度律,梯径理论
刘宇 | 讲者
宋春 | 整理
目录
1. 算法信息论
2. 利用压缩做文本分类
3. 语言建模与压缩是等价的
4. 与智能、生命的联系
近几年来,众多研究者对压缩与智能之间的关系进行了探讨。实际上,探究压缩和智能的联系已有悠久历史,至少可追溯至图灵关于可计算性的研究。此后紧随香农的信息论,1960年代 Solomonoff、Kolmogorov 和 Chaitin 独立提出并发展算法信息论,该领域逐渐引入了诸如柯式复杂度这样的重要概念:即复杂度衡量的是在通用图灵机上生成某个对象的最短程序长度。虽然严格的柯式复杂度是不可计算的,但有效的压缩算法是一种逼近的途径。
将柯式复杂度和压缩算法结合起来,就可以定义出距离。而距离是很多研究的出发点,比如两个词向量意义很接近就是因为它们的距离很近、两个药物分子的功能相近也可能是因为它们本身或某部分之间的距离很近、若干物种间的进化关系也是通过距离构建的。
1. 算法信息论
算法信息论(Algorithmic information theory)是使用理论计算机科学的工具,研究复杂性概念的学科领域。它是信息理论的一环,关注计算与信息之间的关系。按照 Gregory Chaitin 的说法,它是“把香农的信息论和图灵的可计算论放在调酒杯使劲摇晃的结果。”
信息时代的到来

克劳德·香农(Claude Elwood Shannon,1916年4月30日—2001年2月24日),美国数学家、电子工程师和密码学家,被誉为信息论的创始人。香农是密歇根大学学士,麻省理工学院博士。1948年,香农发表了划时代的论文——《通信的数学理论》,奠定了现代信息论的基础。不仅如此,香农还被认为是数字计算机理论和数字电路设计理论的创始人。

达特矛斯夏季人工智能研究计划(Dartmouth Summer Research Project on Artificial Intelligence)由约翰·麦卡锡等人于1956年8月31日发起,旨在召集志同道合的人共同讨论“人工智能”(此定义正是在那时提出的)。会议持续了一个月,基本上以大范围的集思广益为主。这催生了后来人所共知的人工智能革命。会议设定了七个议题,分别为:自动计算机、如何对计算机进行编程以使用语言、神经网络、计算规模理论、自我改进、抽象、随机性与创造性。

到了十九世纪60年代,Solomonoff、Kolmogorov、Chaitin相继发展出算法信息论(Algorithmic Information Theory),他们强调复杂性、信息论与算法之间的关系,算法信息论由此诞生。
第一部分中,我们首先介绍从两个不同角度定义的复杂性:香农熵(信息论角度)、柯式复杂度(算法信息论角度)。再介绍从两个不同角度出发发展出的压缩算法:熵编码压缩(信息论角度)、LZ77压缩算法(算法信息论角度)。最后通过信源编码定理将二者联系起来。
香农熵与柯氏复杂度
下面我们先来引入两个重要概念:香农熵和柯氏复杂度。
香农熵是信息论中的核心概念,用于描述信息的混乱程度,计算如下:
其中Pi为第i类信息出现的频率,但是香农熵缺乏对于信息顺序表征的描述,如“331213221312”和“123123123123”计算所得的香农熵相同。
柯尔莫哥洛夫复杂度(Kolmogorov Complexity)即柯式复杂度,是算法信息论中的核心概念,用于量化对象的复杂性,是指在通用图灵机上最短的信息描述表达。
一些柯氏复杂度的例子:
111111111111 12次重复1
123123123123 4 次重复 123
331213221312 331213221312
172579241727 (3n-2) for n = 1 to 6
然而,柯氏复杂度通常情况下很难找到普适的描述方法。
熵编码压缩
熵编码(Huffman Coding)是一种独立于介质的具体特征进行无损数据压缩的方案。一种主要类型的熵编码方式是对输入的每一个符号,创建并分配一个唯一的前缀码,然后,通过将每个固定长度的输入符号替换成相应的可变长度前缀无关(prefix-free)输出码字替换,从而达到压缩数据的目的。每个码字的长度近似与概率的负对数成比例。因此,最常见的符号使用最短的码。熵编码更偏向于信息论,如果一个字符出现的频率较高,那么我们可以用更少的字符数量去描述。
一种计算方式如下:比如,要描述“this_is_an_ant”,我们先将出现的字符列出,然后统计相应的字符出现频率,从小到大排序,然后将字符按顺序两两叠加在一起。
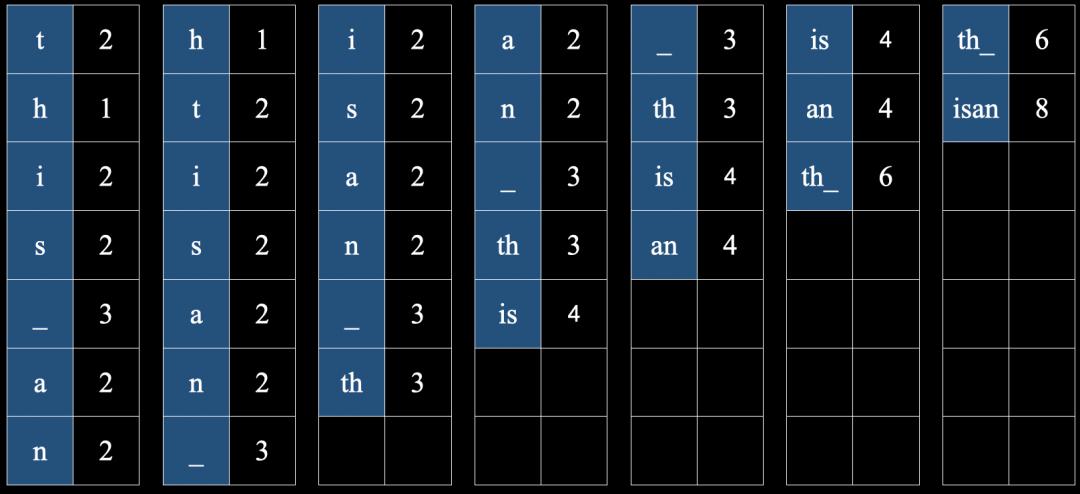
按照字符从组合关系生成一个包含关系的树状图,称之为哈夫曼树(Huffman Tree)。
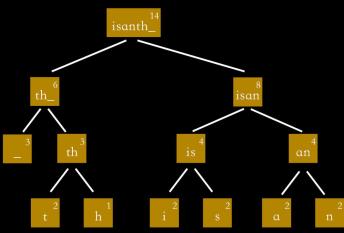
有了哈夫曼树之后,我们将树一侧的分支命名为0,另一侧的分支命名为1:
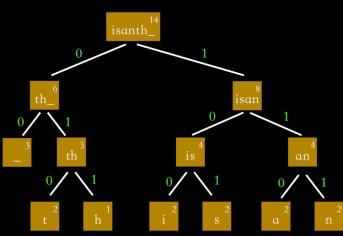
然后依据分支的数字,对每个字符进行相应的编码:
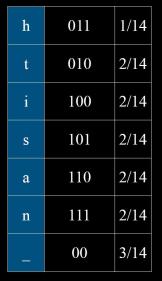
可以发现出现频率最大的字符,我们用最短的编码符号来表示,如“-”采用“00”来编码。
最后,生成哈夫曼编码序列为:
010011100101001001010011011100110111010
这里我们引入一个重要的量——每字符比特(bit per character, bpc),即每个字符需要用多少比特来表示,在这个例子中,“this_is_an_ant” 这14个字符可以用39个01代码来表示,即39个比特(bit)单位,字符每比特大小为:
39/14=2.78471
我们计算这个字符串的香农熵:
信源编码定理(Source coding theorem)表明:无论用任何方法去编码字符串,相应编码的每字符比特(此例子中是2.78471)是不可能小于其香农熵的(此例子中是2.7534)。(后面我们会再看到这个重要的信源编码定理)
LZ77压缩算法
LZ77压缩算法(在1977年由Lempel和Ziv提出)通过使用编码器或者解码器中已经出现过的相应匹配数据信息,替换当前数据从而实现压缩功能。这个匹配信息使用称为长度-距离对的一对数据进行编码,它等同于“每个给定长度字符都等于后面特定距离字符位置上的未压缩数据流”。编码器和解码器都必须保存一定数量的最近的数据,如最近2 KB、4 KB或者32 KB的数据。保存这些数据的结构叫作滑动窗口,因为这样所以LZ77有时也称作滑动窗口压缩。
LZ77编码是算法信息论中的表征,这种编码有两个重要参数:L_window以及L_buffer,我们还以字符串“this_is_an_ant ”为例,在这个例子中将 L_window 和 L_buffer 两个参数分别设为6和5(L_window = 6, L_buffer = 5),代表字符前设置6个空格,缓冲区长度为5,相应的,两个参数设置越大,压缩效率越高。
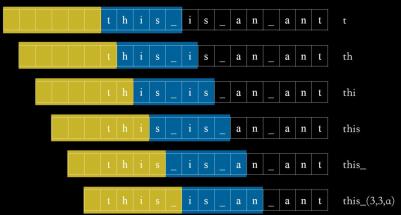
将色块不断向前移动,并且检查缓冲区内是否有与空格区内字符片段重复的部分,本例中,随着缓冲区向前移动,“t”,“th”,“thi”,“this”,“this_”均没有与之前重复,而再向前移动时,“is_”在空格区内有重复部分,我们采用一种三元组(3,3,a)来描述重复部分,在空格区域倒数第3个位置开始,且字段长度为3,重复部分的后续字符为“a”,这样完成重复部分的压缩。显然,当字符串的重复率越高时,压缩效率也越高。
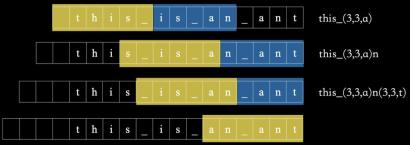
同理,后续部分继续按照这方式压缩,且将每个字符都当成一个三元组,最后的字符串可以表达为:
(0,0,t)(0,0,h)(0,0,i)(0,0,s)(0,0,_)(3,3,a)(0,0,n)(3,3,t)
这是更倾向于柯氏复杂度的一种描述。
压缩完成的三元组可以继续用哈夫曼编码继续压缩,再加上一些技巧,最终一起整合成了著名的Deflate算法(Phil Katz 1989s)。在Deflate算法的基础上改进的gzip算法是平时更加常用的(gzip,Jean-loup Gailly & Mark Adler 1993)。
信源编码定理(Source coding theorem)
信源编码定理表明,在极限情况下,随着独立同分布随机变量数据流的长度趋于无穷,不可能把数据压缩得码率(每个符号的比特的平均数)比信源的香农熵还小,又不丢失信息,香农熵的压缩率是达到信息压缩的极限(Source coding theorem, Shannon 1948)。
然而,在下面的例子中,大家可以看到,用gzip压缩
“this_is_an_antthis_is_an_ant......this_is_an_ant”(重复100次),
其每字符比特达到了0.25,远远小于这个序列的香农熵2.75。难道信源编码定理被打破了吗?大家知道问题出在了哪里?

以上,我们将信息论和算法信息论的背景、基础知识和相应的一些压缩方法做了简单介绍,下面我们看如何用压缩实现文本分类。
2. 利用压缩做文本分类
文本分类的方法
最近的一篇文章[1]发现 gzip + k-nearest neighbors (kNN) 方法与大语言模型是差不多的,gzip 我们已经提到,是基于LZ77的一种压缩算法,kNN是机器学习中的最邻近法(k-nearst neighbors),新文本依据其和既有文本的距离来判断其类型。
[1] “Low-Resource” Text Classification: A Parameter-Free Classification Method with Compressors
https://aclanthology.org/2023.findings-acl.426/
那么如何通过压缩来定义文本之间的距离呢?——通过压缩!Gzip本质上是一种压缩机,可以实现对文本的压缩,这里我们有这样一种直觉,两篇文章进行压缩时,如果文章是相同类型的,那么可压缩的部分是相当多的,可以获取较高的压缩率,而当两篇文章内容相差很大,属于不同类型时,相应的压缩率就会很低,这样通过压缩率的高低,我们可以判断文本之间的距离。
如何用压缩定义距离?
早在1998年,Bennett等人[2]就介绍了如何用柯式复杂度定义距离:
其中,K(x|y)为用文本y压缩后的信息区压缩x的柯氏复杂度,K(y|x)为用文本x压缩后的信息区压缩y的柯氏复杂度,这两者的最大值即为文本x和y之间的距离,然而,柯氏复杂度是无法计算的。
[2] 1998, Charles Bennett, Peter Gacs, Ming Li, Paul Vitanyi, Wojciech Zurek , Information Distance
https://arxiv.org/abs/1006.3520
2004年,Li Ming等提出了更实用的NCD方法(Normalized Compression Diatance)[3]:
用压缩机的压缩距离区逼近柯氏复杂度。
[3] 2004, Ming Li, Xin Chen, Xin Li, Bin Ma, Paul Vitanyi , The similarity metric
https://ieeexplore.ieee.org/document/1362909
任意一个压缩机都行吗?不是的。要能比较好地逼近柯氏复杂度,这个压缩机必须有一些优良的性质。简单起见,这里只提其中一个性质,即强分配律(Distributivity):
C(xyz)+C(z) ≤ C(xz)+C(yz)
这个强分配率可弱化为弱分配律:
C(xy)+C(z) ≤ C(xz)+C(yz)
进一步弱化,即为次可加性(Subadditivity)(将弱分配律中z设为空字符,即得到次可加性)
C(xy) ≤ C(x)+C(y)
我们验证过,gzip一般很难满足强分配律的,很多情况下满足弱分配律但偶尔也不满足,次可加性一般都是可以满足的(严格意义上的“柯氏压缩机”需要满足强分配律)。但是gzip作为一种逼近方法,也还算是一个效果还不错的压缩机。当然,满足更强条件的压缩机会更好的。
使用压缩机定义完距离之后,分类问题就容易了(大模型的语义其实本质上就是词向量之间的距离)。2005年压缩被用于分类[4],这时候并没有大模型出现,文章做了一些小的数据集,如进行语言的分类,音乐的分类、蛋白质的分类、物种的分类。
[4] 2005, Rudi Cilibrasi, Paul Vitanyi,Clustering by compression
https://arxiv.org/abs/cs/0312044
在此背景下,文章[5]采用不同模型在不同的数据集上进行训练来进行文本分类,gzip+kNN 达到了相当好的效果,基本上可以与大模型相当。
[5] Low-Resouree Text Classification: A Parameter-Free ClassificationMethod with compressors
https://aclanthology.org/2023.findings-acl.426/
PS:然而并不是压缩率越高,分类效果越好,bz2 也是一类常用的压缩机,压缩率要高于gzip,但是bz2已经将文本语义打乱了,分类效果反而很差。
梯径(Ladderpath)方法
算法信息论框架下的梯径(Ladderpath)方法也是可以实现压缩的,而且我们发现效果比上述文章好。这是我们课题组自己的研究工作(这里不做详细介绍,如有需要可以联系笔者)。
3. 语言建模与压缩是等价的

近年来,机器学习社区一直专注于训练日益庞大和强大的语言模型,这些模型表现出令人印象深刻的预测能力。2024年5月的文章 Language Modeling Is Compression 介绍了如何将语言模型用于无损压缩,反之亦可。作者主张通过压缩的角度来观察预测问题,并评估语言模型的压缩能力。结果表明,大型语言模型是强大的通用预测器。压缩观点提供了对智能、标度律、标记化(tokenization)和上下文学习的新见解。

文章 Language Modeling Is Compression 作者之一“大神”Marcus Hutter在2006年发起了著名的信息压缩竞赛——“500 000€ Prize for Compressing Human Knowledge”。他坚定地认为“压缩即智能”。
“虽然智能是一个模糊的概念,但文件大小是硬数字。维基百科是人类知识的广泛快照。如果你能比你的前辈更好地压缩维基百科的前1GB,你的压缩(解压缩)器很可能是更加智能的。该奖项的目的是鼓励开发智能压缩机/程序,以此作为通往AGI的道路。”
事实上,在2023年4月 DeepMind 的创始人之一 Ilya Sutskever 以及 Jack Rae 也讨论过柯氏复杂度、压缩机以及大语言模型之间的关系。

以上的研究表明,语言建模和压缩可能是等价的,大语言模型是可以用来进行无损压缩的。如果一个压缩机可以完美地达到柯氏复杂度的极限,那么它很可能就是AGI。虽然数学证明表明,柯氏复杂度不可达到的,但是可以无限趋近,gzip本身是一类很好的压缩机,但是用语言模型压缩是一类更加有效的方法。
算术编码
下面我们从具体案例出发,看一下大模型究竟是如何实现压缩的,这部分内容仍然来自文章 Language Modeling Is Compression。首先,算术编码(Arithmetic Coding)也是一种熵编码,它依据字符出现次数的频率来进行编码,这个过程可以用语言模型来实现。
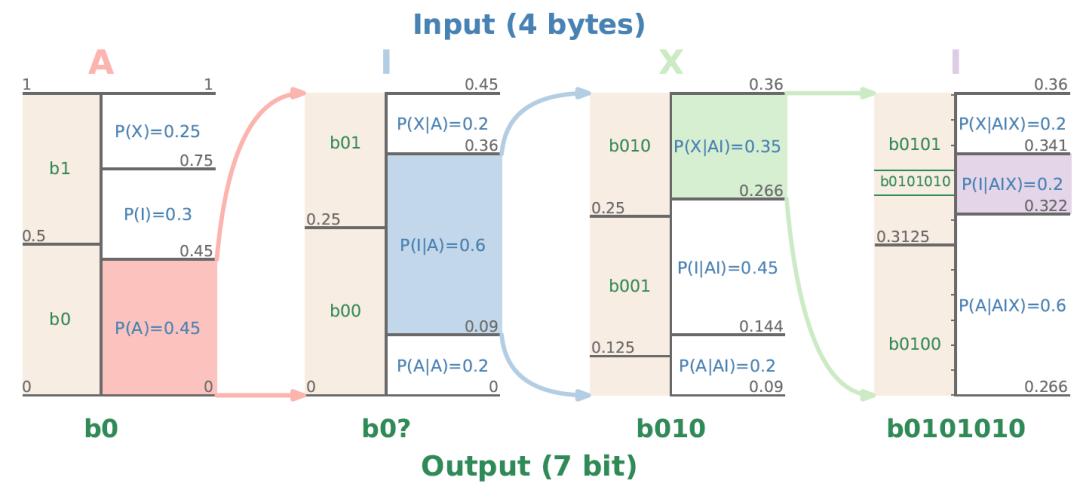
比如,对字符串 “AIXI” 进行压缩,首先对第一个字符“A”进行概率计算,然后在第一个字符为“A”的情况下,计算第二个字符为“I”的条件概率,后续依次继续计算“X”和“I”,最终得到整体分布的概率区间。(这里是一个非常粗糙的概述,详细了解可观看读书会分享)
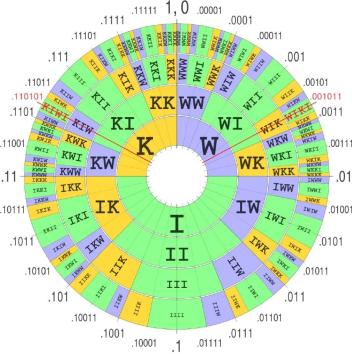
相应地,字符串越长,得到的概率区间就越精细,越靠近上面圆盘的边缘位置,压缩完成后得到的是一个位于0-1之间的概率区间,如“AIXI”在本例中压缩为区间 [0.322, 0.341)。

得到的概率区间可以进一步进行压缩,得到01字符串,本例中,“AIXI”最终压缩为0101010。
那么大模型与压缩之间的关系是什么呢?——是条件概率!我们可以通过大模型很好地预测token的条件概率,然后基于这些条件概率来实现后续压缩。通过大模型,可以实现远高于传统压缩技术的压缩率。
标度律(Scaling law)
从结果来看,利用语言模型进行算术编码(Arithmetic Encoding)的压缩率比传统压缩技术高很多(但是要剔除模型规模的影响)。文中对传统方法(gzip、LZMA2、PNG、FLAC)和语言模型方法在不同数据集上进行了实验,结果如下(注意,一般所说的压缩率是指(1-压缩后文本长度 / 原长度),而文中的compression rate其实是指(1-压缩率);为了避免歧义,我们称其为压缩后比例):
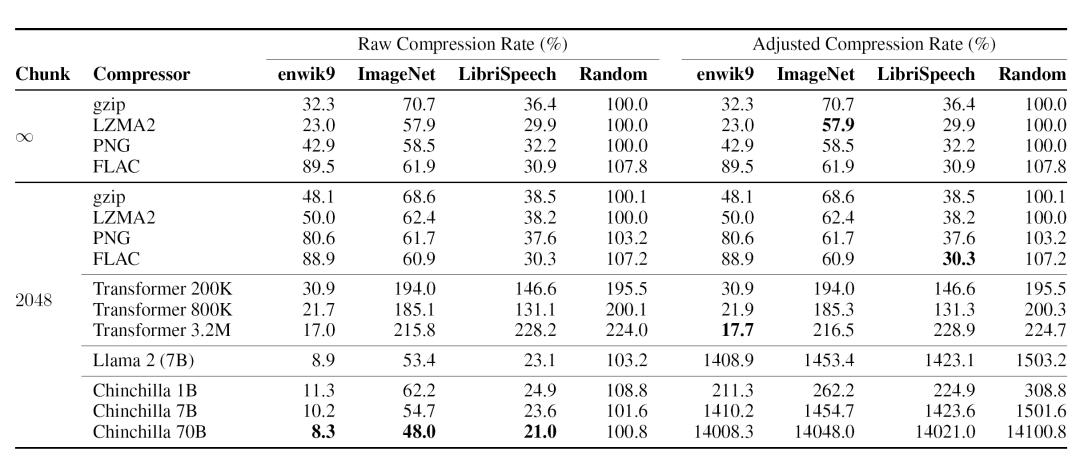
大模型的压缩率是高于传统的压缩方法的,大模型使用的参数越多,相应的压缩率就越高,在各个数据集上都呈现相似的规律。
事实上,我们可能需要考虑模型本身的大小,即矫正后的压缩后比例(Adjusted Compression Rate)。对于传统方法来讲,压缩率几乎是不变的,大模型巨量的参数信息使得总的压缩率大大提升,甚至达到了原始压缩数据体积的数倍乃至数百倍。
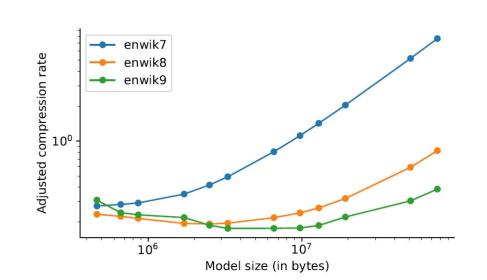
进一步的研究发现,较大规模的模型,其压缩效果会更好,这一现象一般被称为标度律(Scaling law)。然而当模型的规模超过一定限度继续增大时,压缩效果会变差,压缩后比例会增加。另一方面,大规模模型在较小的数据集上实现的压缩效果较差,所以模型规模并不是越大越好。文章最后总结说,数据集大小直接限制了模型规模,标度律实际上也取决于测试集的大小;对于一定规模的数据集,模型会有一个效果最好的极值。
最后值得提一点,文章中也同样用压缩机(比如gzip)做了生成任务。虽然文中也承认其效果一般,但是可以进一步探索。正是由于可以用大模型做无损压缩,反过来,也可以用压缩机来做生成,所以文章说语言建模和压缩是等价的,也就是“压缩即智能”。
4. 与智能、生命的联系
由以上压缩与大模型的关系,压缩与智能、生命的联系也是值得探寻的。
这里简要介绍几篇文章。在文章 Symmetry and simplicity spontaneously emerge from the algorithmic nature of evolution 中说到:对称性与简单性是可以从自然进化中自发地演化出来的,不需要一个选择过程。工程设计中也总是采用模块化以及对称性,生命系统中蛋白的柯氏复杂度较高的蛋白是很少的。
作者引入了一种基于进化算法视角的非适应性假说:对称结构的优先产生不仅是由于自然选择,还因为它们需要更少的特定信息来编码,因此更有可能通过随机突变作为表型变异出现。对称性的偏好是这种对可压缩描述偏向的一个特例;较低的描述复杂度也与更高的突变鲁棒性相关。这可能有助于复杂模块化多组件组装的进化。
[6] Symmetry and simplicity spontaneously emerge from the algorithmic nature of evolution
https://www.pnas.org/doi/full/10.1073/pnas.2113883119
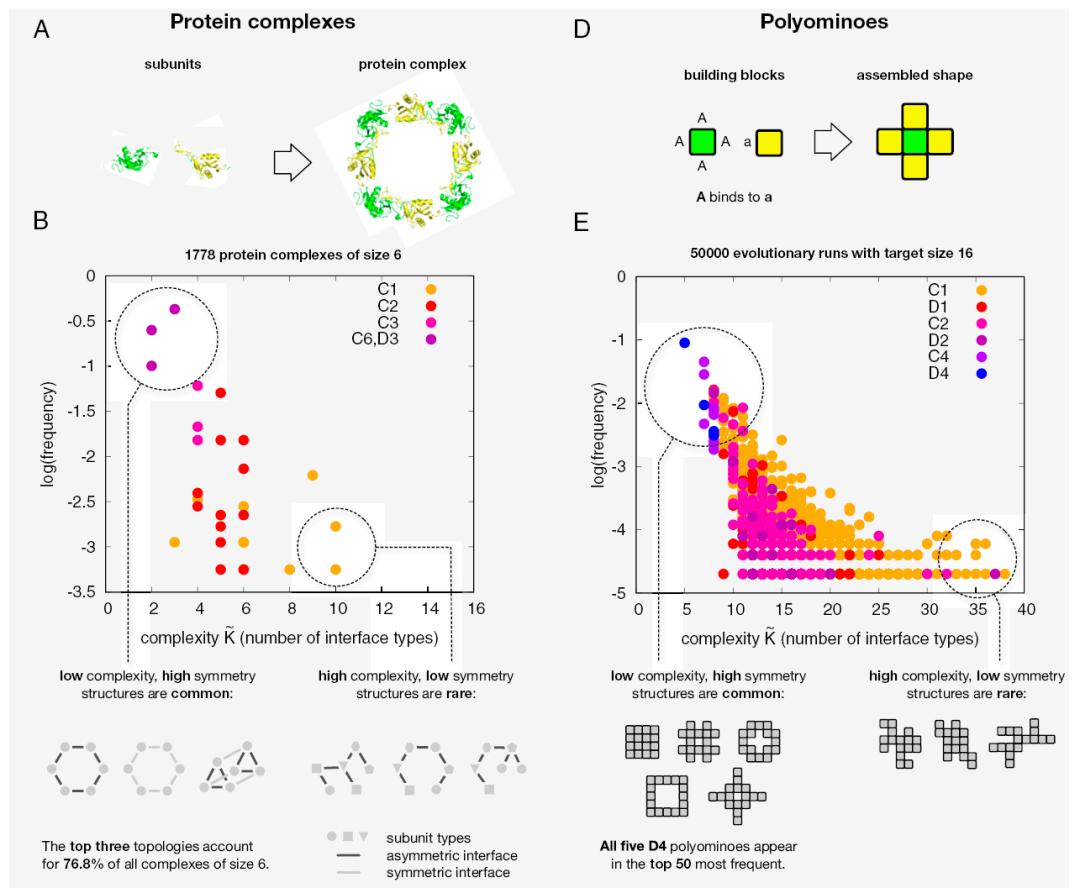
对称表型通常需要较少的信息进行算法编码,因为存在子单元的重复。这种更高的可压缩性减少了对基因型的限制,这意味着更多的基因型会映射到更简单、更对称的表型,而不是更复杂的不对称表型。在随机突变中,这些对称表型更有可能作为潜在变异出现,因此,即使没有自然选择对对称性的选择,也可能出现强烈的对称性偏向。
2022年的文章 Hallucinating symmetric protein assemblies 用大模型的幻觉去设计大蛋白。只需要设定亚基数目和蛋白长度,就可以生成很多具有对称结构的蛋白质,而且有些已经被真实地制造出来。

[7] Hallucinating symmetric protein assemblies
https://www.science.org/doi/10.1126/science.add1964
4. 总结
至此,本文主要回顾了算法信息论的一些基础概念,信息的一些压缩方式,以及压缩与语言模型之间的关系,发现压缩与语言模型是等价的,一些极具价值的文献在文章中探讨,最后我们浅谈了压缩与生命、智能的关系。我们简要提到自己的工作,在算法信息论框架下的梯径(Ladderpath)方法(这里没有做详细介绍,如有需要可以参考下面几篇关于梯径理论的文章,或者联系笔者)。
Z Xu, …, Y Liu*, Correlating measures of hierarchical structures in artificial neural networks with their performance, npj Complexity (in press)
Z Zhang, …, Y Liu*, Evolutionary tinkering enriches the hierarchical and nested structures in amino acid sequences, Physical Review Research, 6:023215, 2024.
Yu Liu*, et al., Ladderpath approach: How tinkering and reuse increase complexity and information, Entropy, 24(8): 1082, 2022.
Yu Liu, et al., Exploring and mapping chemical space with molecular assembly trees, Science Advances, 7: eabj2465, 2021.
关于梯径理论的文章:
学者简介
刘宇,副教授,北京师范大学珠海校区-文理学院系统科学系-Evolving Complex Systems Lab。目前研究方向:用算法信息论研究生命的起源与演化,即,把生命系统定量刻画成软件系统。
原标题:《为什么“压缩即智能”?算法信息论与大模型、生命、智能的联系》